Πώς να καθορίσετε την ακτίνα ενός κύκλου, γνωρίζοντας το μήκος του
Πώς να καθορίσετε την ακτίνα ενός κύκλου, γνωρίζοντας το μήκος του
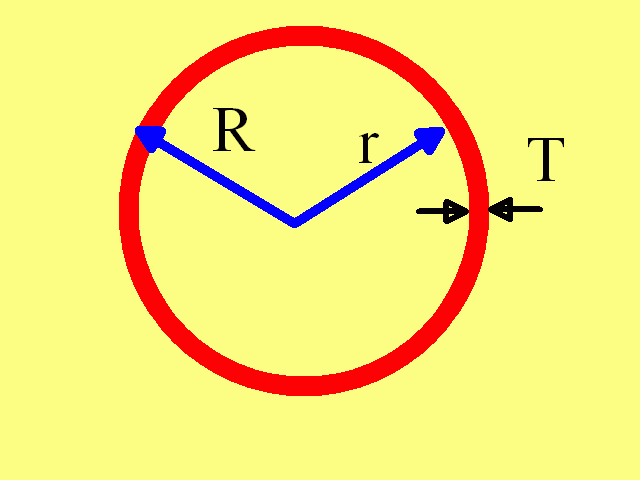
Συνήθως σε γεωμετρικά προβλήματα η ακτίνα είναι γνωστή,και πρέπει να υπολογίσετε το μήκος του κύκλου. Αλλά μπορεί να υπάρχει μια αντίθετη κατάσταση, όταν για ένα δεδομένο μήκος ενός κύκλου είναι απαραίτητο να καθοριστεί πόσο μακριά θα είναι από το κέντρο, δηλαδή, για να υπολογίσει την ακτίνα.

"Διδάσκουν στο σχολείο, διδάσκουν στο σχολείο ..."
Στο πρόγραμμα σπουδών της έκτης τάξης, φοιτητέςτα γενικά σχολεία κατά τη διάρκεια της γεωμετρίας μελετούν τον κύκλο και τον κύκλο ως γεωμετρικό σχήμα και όλα όσα σχετίζονται με αυτό το σχήμα. Οι τύποι γνωρίζουν με τέτοιες έννοιες την ακτίνα και τη διάμετρο, την περιφέρεια ή την περίμετρο του κύκλου, την περιοχή του κύκλου. Είναι σε αυτό το θέμα που μαθαίνουν για τον μυστηριώδη αριθμό Pi - αυτός είναι ο αριθμός ludolph, όπως ονομάστηκε πριν. Ο αριθμός Pi είναι παράλογος, αφού η αναπαράστασή του με τη μορφή ενός δεκαδικού κλάσματος είναι άπειρη. Στην πράξη, χρησιμοποιείται η περικομμένη έκδοση των τριών ψηφίων: 3.14. Αυτή η σταθερά εκφράζει τον λόγο του μήκους οποιουδήποτε κύκλου προς τη διάμετρο του. Οι έξι γκρέιντερ επιλύουν προβλήματα, αφαιρώντας για ένα δεδομένο και αριθμούς "Pi" άλλα χαρακτηριστικά ενός κύκλου και ενός κύκλου. Στα σημειωματάρια και σε ένα μαυροπίνακα, κλιμακώνουν τις αφηρημένες σφαίρες σε μια κλίμακα και παράγουν ελάχιστα λεγόμενους υπολογισμούς. Και στην πράξη
Στην πράξη, αυτό το έργο μπορεί να προκύψει στομια κατάσταση όπου, για παράδειγμα, υπάρχει ανάγκη να κατασκευαστεί ένα κομμάτι ορισμένου μήκους για κάθε διαγωνισμό με την αρχή και το τέλος σε ένα μέρος. Υπολογίζοντας την ακτίνα, μπορείτε στο πλάνο να επιλέξετε το πέρασμα αυτής της διαδρομής με μια πυξίδα στο χέρι, λαμβάνοντας υπόψη τις επιλογές που λαμβάνουν υπόψη τα γεωγραφικά χαρακτηριστικά της περιοχής. Μετακινώντας το πόδι της πυξίδας - ένα ισότιμο κέντρο από τη μελλοντική διαδρομή, είναι ήδη δυνατόν σε αυτό το στάδιο να παράσχετε όπου τα οικόπεδα θα βρίσκονται στις πλαγιές, όπου οι πλαγιές, λαμβάνοντας υπόψη τις φυσικές διαφορές στο έδαφος. Επίσης, μπορείτε να αποφασίσετε αμέσως για τις περιοχές όπου είναι καλύτερο να τοποθετήσετε τις βάσεις για τους οπαδούς. Ακτίνα από τον κύκλο
Υποθέστε ότι εσείς(R) κύκλος με γνωστό μήκος (C): R = C / 2n (n είναι ένας αριθμός ίσος με 3.14) Με τον καθορισμό των διαθέσιμων τιμών, μπορείτε να πάρετε εύκολα το αποτέλεσμα: R = 10 000: 3.14 = 3 184. 71 (m) ή 3 km 184 m και 71 cm. Από την ακτίνα στην περιοχή
Γνωρίζοντας την ακτίνα του κύκλου, είναι εύκολο να προσδιοριστείτην περιοχή που θα αφαιρεθεί από το τοπίο. Ο τύπος της περιοχής του κύκλου (S): S = nR2 Για R = 3 184. 71 m, θα είναι: S = 3.14 x 3 184. 71 x 3 184. 71 = 31 847 063 (sq. M) ή σχεδόν 32 τετραγωνικά χιλιόμετρα. Τέτοιοι υπολογισμοί μπορεί να είναι χρήσιμοι για την περιφράγιση. Για παράδειγμα, έχετε υλικό για το φράκτη για όσα γραμμικά μέτρα. Λαμβάνοντας αυτή την τιμή για την περίμετρο του κύκλου, μπορείτε εύκολα να καθορίσετε τη διάμετρο (ακτίνα) και την περιοχή και, κατά συνέπεια, να αναπαριστάτε οπτικά την αξία της μελλοντικής περιφραγμένης περιοχής.