Συμβουλή 1: Βρείτε τις γωνίες ενός κανονικού πολυγώνου
Συμβουλή 1: Βρείτε τις γωνίες ενός κανονικού πολυγώνου
Τα σωστά πολύγωνα βρίσκονται στη ζωήκάθε μέρα, για παράδειγμα, ένα τετράγωνο, ένα τρίγωνο ή ένα εξάγωνο με τη μορφή του οποίου όλες οι κηρήθρες γίνονται. Για να κατασκευάσετε τον εαυτό σας κανονικό πολύγωνο, πρέπει να το ξέρετε γωνίες.

Οδηγίες
1
Αρχικά, χρησιμοποιώντας τον τύπο S = 180⁰ (n-2), υπολογίστε το άθροισμα των εσωτερικών γωνιών του πολύγωνο. Για παράδειγμα, αν θέλετε να βρείτε γωνίες σωστά πολύγωνο με 15 πλευρές, αντικαταστήστε n = 15 στην εξίσωση. Θα πάρετε S = 180⁰ (15-2), S = 180⁰χ13, S = 2340 </ s>.
2
Στη συνέχεια, διαιρέστε το προκύπτον άθροισμα των εσωτερικών γωνιώναπό τον αριθμό τους. Για παράδειγμα, στο παράδειγμα πολυγώνου, ο αριθμός των γωνιών είναι ίσος με τον αριθμό των πλευρών, δηλαδή 15. Έτσι, παίρνετε ότι η γωνία είναι 2340⁰ / 15 = 156⁰. Κάθε εσωτερική γωνία πολύγωνο είναι ίσο με 156 </ s>.
3
Εάν προτιμάτε να υπολογίσετε γωνίες πολύγωνο σε ακτίνια, προχωρήστε ως εξής. Αφαιρέστε τον αριθμό 2 από τον αριθμό των πλευρών και πολλαπλασιάστε τη διαφορά που προκύπτει από τον αριθμό P (Pi). Στη συνέχεια διαιρέστε το προϊόν από τον αριθμό των γωνιών στο πολύγωνο. Για παράδειγμα, εάν πρέπει να υπολογίσετε γωνίες διορθώστε 15-gon, ενεργήστε ως εξής: Π * (15-2) / 15 = 13 / 15Π, ή 0,87Π, ή 2,72 (αλλά, κατά κανόνα, ο αριθμός Π παραμένει αμετάβλητος). Ή απλά διαιρέστε το μέγεθος της γωνίας σε μοίρες κατά 57,3 - ακριβώς όπως πολλοί βαθμοί περιέχονται σε ένα radian.
4
Μπορείτε επίσης να προσπαθήσετε να υπολογίσετε γωνίες σωστά πολύγωνο στην πόλη. Για να το κάνετε αυτό, αφαιρέστε 2 από τον αριθμό των πλευρών, διαιρέστε τον αριθμό με τον αριθμό των πλευρών και πολλαπλασιάστε το αποτέλεσμα κατά 200. Αυτή η μονάδα γωνιών σχεδόν δεν χρησιμοποιείται σήμερα, αλλά αν αποφασίσετε να μετρήσετε γωνίες στο χαλάζι, μην ξεχνάτε ότι το χαλάζι διασπάται σε μερικά δευτερόλεπτα και λεπτά (100 δευτερόλεπτα ανά λεπτό).
5
Ίσως πρέπει να υπολογίσετε την εξωτερική γωνία του δεξιού πολύγωνο, στην προκειμένη περίπτωση, να το πράξουν. Αφαιρέστε την εσωτερική γωνία από 180 - - ως αποτέλεσμα έχετε την αξία της γειτονικής, δηλαδή της εξωτερικής γωνίας. Μπορεί να πάρει μια τιμή από -180⁰ έως + 180⁰.
Συμβουλή 2: Πώς να βρείτε τον αριθμό των πλευρών ενός πολυγώνου
Το πολύγωνο αποτελείται από πολλά τμήματα,συνδέονται μεταξύ τους και σχηματίζουν μια κλειστή γραμμή. Όλα τα στοιχεία της κατηγορίας αυτής χωρίζονται σε απλά και πολύπλοκα. Ένα απλό τρίγωνο και ένα τετράπλευρο, και σε σύνθετα - πολύγωνα με μεγάλο αριθμό συμβαλλόμενα μέρη, καθώς και πολυγώνια σε σχήμα αστεριού.
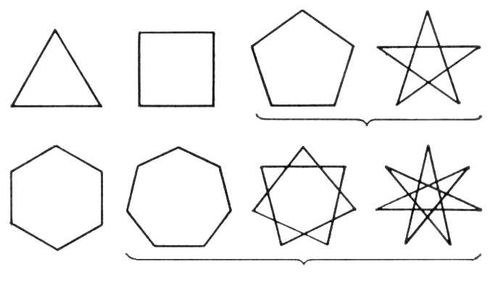
Οδηγίες
1
Τα πιο συχνά συναντώμενα προβλήματα είναι το κανονικό τρίγωνο ω συμβαλλόμενα μέρηΩ α. Δεδομένου ότι το πολύγωνο είναι κανονικό, και τα τρία από αυτά συμβαλλόμενα μέρηs είναι ίσα. Επομένως, γνωρίζοντας το διάμεσο και το ύψος του τριγώνου, μπορείτε να βρείτε όλα αυτά συμβαλλόμενα μέρηs. Για να το κάνετε αυτό, χρησιμοποιήστε τη μέθοδο εύρεσης συμβαλλόμενα μέρηs μέσω του ημιτονοειδούς: a = x / cosα συμβαλλόμενα μέρηΤα τρίγωνα είναι ίσα, δηλ. a = b = c = a, a = b = c = x / cosα, όπου το x είναι το ύψος, το διάμεσο ή το bisector. συμβαλλόμενα μέρηs σε ισοσκελές τρίγωνο, αλλά κάτω από μία προϋπόθεση - ένα δεδομένο ύψος. Θα πρέπει να προβάλλεται στη βάση του τριγώνου. Γνωρίζοντας το ύψος της βάσης x, βρείτε συμβαλλόμενα μέρηγια ένα ισοσκελές τρίγωνο a: a = x / cosα.Αφού a = b, δεδομένου ότι το τρίγωνο είναι ισοσκελές, βρείτε το συμβαλλόμενα μέρηs ως εξής: a = b = x / cosα Αφού βρείτε το πλάγιο συμβαλλόμενα μέρη(x / cosa) ^ 2 (x ^ 2) = √x ^ 2 (1-cos ^ 2α) / cos ^ 2α, υπολογίστε το μήκος της βάσης του τριγώνου, εφαρμόζοντας το θεώρημα Pythagorean = xtgα Από εδώ, βρείτε τη βάση: c = 2xtgα.
2
Η πλατεία είναι ένα κανονικό τετράπλευρο, συμβαλλόμενα μέρητα οποία υπολογίζονται με διάφορους τρόπους. Κάθε ένα από αυτά συζητείται παρακάτω. Ο πρώτος τρόπος είναι να βρεθεί συμβαλλόμενα μέρηs σε όλη τη διαγώνιο της πλατείας. Δεδομένου ότι όλες οι γωνίες ενός τετραγώνου είναι ευθείες, αυτή η διαγώνια τους χωρίζει κατά το ήμισυ με τέτοιο τρόπο ώστε δύο ορθογώνια τρίγωνα με γωνίες 45 μοιρών σχηματίζονται στη βάση. Κατά συνέπεια, συμβαλλόμενα μέρηκαι το τετράγωνο είναι: a = b = c = f = d * cosα = d√2 / 2, όπου d είναι η διαγώνιος του τετραγώνου. συμβαλλόμενα μέρηy: a4 = R√2, όπου R είναι η ακτίνα του κύκλου.
3
Κάνε πολλάσυμβαλλόμενα μέρητα πολύγωνα τους συμβαλλόμενα μέρηy υπολογίστε την τελευταία από τις προτεινόμενες μεθόδους - πληκτρολογώντας πολύγωνο σε έναν κύκλο. Για να γίνει αυτό, σχεδιάστε ένα κανονικό πολύγωνο με αυθαίρετο συμβαλλόμενα μέρηκαι γύρω από αυτό περιγράφει έναν κύκλο με μια δεδομένη ακτίνα R. Φανταστείτε ότι ένα αυθαίρετο n-gon δίνεται στο πρόβλημα. Εάν περιγράφεται ένας κύκλος κοντά σε αυτό πολύγωνο, τότε για να βρούμε συμβαλλόμενα μέρηΧρησιμοποιήστε τον τύπο: an = 2Rsinα / 2.
Συμβουλή 3: Τι είναι το Πολύγωνο Ανταγωνιστικότητας;
Η ανταγωνιστικότητα είναι μια έννοια,χαρακτηρίζοντας τις δυνατότητες του αντικειμένου ή του αντικειμένου της παραγωγής να υπερβαίνουν τα ανάλογα στις υπάρχουσες συνθήκες. Οι πληροφορίες σχετικά με αυτόν τον δείκτη συμβάλλουν στη δημιουργία μιας πραγματικής εικόνας της ζήτησης για το προϊόν.

Οι πληροφορίες αυτές συμβάλλουν στην εμφάνιση τουδιευθύνοντας την περαιτέρω ανάπτυξη των επιχειρήσεων και τον σχηματισμό της ετοιμότητας για αλλαγή. Το τελευταίο είναι εξαιρετικά σημαντικό για την ταχεία προσαρμογή στις νέες συνθήκες. Οι επενδυτές, οι καταναλωτές, οι παραγωγοί, το κράτος εφαρμόζουν μια ποικιλία μεθόδων για την αξιολόγηση της ανταγωνιστικότητας. Φυσικά, κάθε ένα από τα θέματα πραγματοποιεί ανάλυση βασισμένη στην κερδοφορία στις συνθήκες της σύγχρονης αγοράς. Για παράδειγμα, ένας επενδυτής που επιλέγει ένα αντικείμενο συνημμένου αναλύει τον βαθμό ελκυστικότητας μιας περιοχής ή μιας συγκεκριμένης επιχείρησης. Εξετάζεται επίσης η καταλληλότητα των επενδύσεων που έχουν ήδη πραγματοποιηθεί. Οι μέθοδοι προσδιορισμού του βαθμού ανταγωνιστικότητας θα πρέπει να λαμβάνουν υπόψη τα ποιοτικά χαρακτηριστικά των προϊόντων, την αναλογία των τιμών με τα ανάλογα, το επίπεδο εξυπηρέτησης των πελατών, την αποτελεσματικότητα των εφαρμοζόμενων τεχνολογιών διαφήμισης.







